Diffusion maps in search of outliers of polarization curves
DOI:
https://doi.org/10.14295/vetor.v32i1.13500Keywords:
Diffusion Maps, Outliers, Polarization curvesAbstract
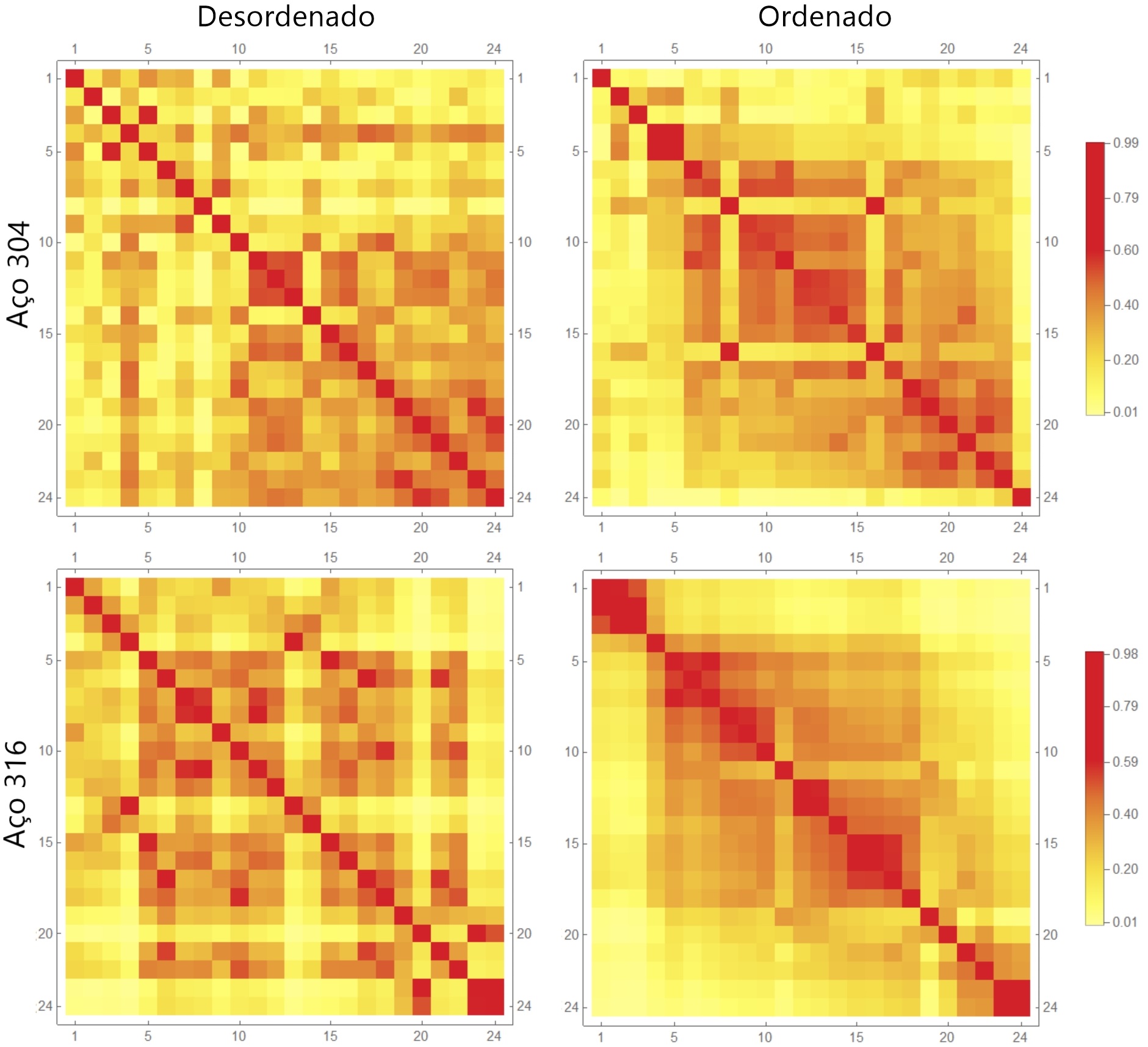
This work proposes an efficient nonlinear dimensionality reduction technique known as Diffusion Maps in the identification of polarization curve outliers. Such curves evaluate the global kinetics of electrochemical electrode processes in corrosive media under steady-state conditions. However, they can present scattering of experimental nature or due to artifacts that may occur. Thus, a search for outliers is necessary because it would allow extracting them from the set of experimental curves under analysis; eventually, they do not adequately translate the material's behavior immersed in the corrosive environment to a given electrochemical potential. The hope is to achieve a good classification rate, eliminating improbable results from the data. However, classifying them correctly is a challenge because a strong nonlinearity typical of polarization curves besides the overlap make the task difficult. In this work, two stainless steels were studied in an aqueous solution with 3.5 % NaCl. Through the diffusion matrix and the associated color map, the Diffusion Maps technique was able to satisfactorily find outliers for both steels used, proving useful because of the proposed approach.
Downloads
References
R. Fabbri, I. N. Bastos, F. D. M. Neto, F. J. Lopes,W. N. Gonçalves, e O. M. Bruno, “Multi-q pattern classification of polarization curves,” Physica A: Statistical Mechanics and its Applications, vol. 395, pp. 332–339, 2014. Disponível em: https://doi.org/10.1016/j.physa.2013.09.048
G. Wang, J. Liu, Y. Li, e L. Shang, “Fault detection based on diffusion maps and k nearest neighbor diffusion distance of feature space,” Journal of Chemical Engineering of Japan, vol. 48, no. 9, pp. 756–765, 2015. Disponível em: https://doi.org/10.1252/jcej.14we227
F. M. Neto, P. Souza, e M. de Magalhães, “Determining baseline profile by diffusion maps,” European Journal of Operational Research, vol. 279, no. 1, pp. 107–123, 2019. Disponível em: https://doi.org/10.1016/j.ejor.2019. 05.032
R. R. Coifman e S. Lafon, “Diffusion maps,” Applied and Computational Harmonic Analysis, vol. 21, no. 1, pp. 5–30, 2006. Disponível em: https://doi.org/10.1016/j.acha.2006.04.006
R. R. Coifman e M. J. Hirn, “Diffusion maps for changing data,” Applied and Computational Harmonic Analysis, vol. 36, no. 1, pp. 79–107, 2014. Disponível em: https://doi.org/10.1016/j.acha.2013.03.001
S. S. Lafon, “Diffusion maps and geometric harmonics,” Tese de doutorado, Yale University, New Haven, Estados Unidos, 2004. Disponível em: https://sites.google.com/site/stefansresearchpapers/
Downloads
Published
Versions
- 2022-08-03 (3)
- 2022-07-15 (2)
- 2022-07-15 (1)















